Comenzamos el curso de nuevo. Ya hace unos nueve años que conozco lo que son las estructuras de datos avanzadas para la programación, pero no obstante, qué le vamos a hacer, hay que sacarse los estudios y me toca profundizar un poco en este tipo de datos. He pensado que, para hacer más llevadero el estudio, voy a comenzar a publicar aquí mis apuntes, así, además de tenerlos siempre disponibles, los comparto.
Definiciones
Los grafos son nodos (o vertices) unidos por líneas (o aristas). Según las aristas podemos encontrarnos grafos no dirigidos o grafos dirigidos, según si las aristas tienen dirección o no.
Un ejemplo de grafo no dirigido:
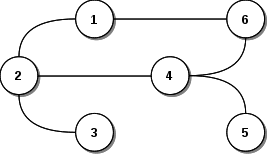
La forma de representar el gráfo en modo de ecuación es G = (N, A), siendo N(G) el conjunto de nodos (vértices) y A(G) el conjunto de aristas del grafo. La representación del grafo de ejemplo sería el siguiente:
N(G) = { 1, 2, 3, 4, 5, 6 }
A(G) = { (1,2), (1,6), (6,4), (4,5), (2,3), (2,4) }Una arista que se enlaza un nodo consigo mismo se la denomina bucle o lazo.
Dos nodos son adyacentes si siendo distintos existe una arista que los une.
El grado de un vértice (o nodo) es el número de aristas que entran o salen de él.
Un camino es una secuencia de aristas consecutivas. La longitud del camino corresponde al número de aristas que contiene. Hay dos tipos de caminos:
- camino simple, es un camino que no emplea más de una vez la misma arista;
- camino compuesto, cuando el camino emplea dos veces la misma arista (aunque no de forma continua).
Un ciclo (o circuito) es un camino simple que empieza y termina en el mismo vértice.
Un ejemplo de grafo dirigido:
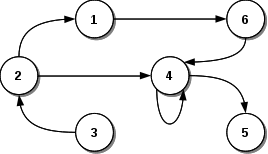
La forma de representar el gráfo en modo de ecuación es G = <N, A>, siendo N<G> el conjunto de nodos (vértices) y A<G> el conjunto de aristas del grafo. La representación del grafo de ejemplo sería el siguiente:
N(G) = { 1, 2, 3, 4, 5, 6 }
A(G) = { <2,1>, <1,6>, <6,4>, <4,5>, <3,2>, <2,4>, <4,4> }El grado de un vértice (o nodo) en el grafo dirigido, puede ser de:
- grado de entrada (o entrante) de un vértice que es el número de aristas que llegan a él (con dirección hacia él); y el
- grado de salida (o saliente) de un vértice que es el número de aristas que salen de él (con dirección hacia otros vértices).
Un camino, en un grafo dirigido, es una secuencia finita de aristas entre dos vértices, siendo el extremo final de cada arista el extremo inicial de la siguiente.
Un grafo dirigido es fuertemente conexo si para cada par de vértices distinos n y m hay un camino de n a m y viceversa. El grafo dirigido expuesto como ejemplo tiene esta propiedad, ya que se puede acceder a cualquier nodo desde cualquier otro.
Dos vértices o nodos están conectados si hay un camino que los une.
Las aristas, al igual que los vértices, también pueden contener información, este es el caso de los grafos etiquetados (o valorados). Se representan de la siguiente forma:
G = (N,A,P)
N(G) = { 1, 2, 3, 4, 5, 6 }
A(G) = { <2,1>, <1,4>, <4,3>, <3,2>, <2,4>, <4,5>, <6,4> }
P(G) = { 5, 8, 1, 10, 2, 6, 7 }La representación gráfica:
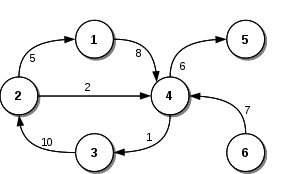
Tipos de Grafos
Realizando, según sus propiedades, una categorización de grafos podemos distinguir los siguientes tipos:
- grafo no dirigido, es un grafo cuyas aristas no tienen dirección.
- grafo dirigido, es un grafo cuyas aristas tienen dirección;
- grafo nulo, es un grafo sin vérticos (y por ende, sin aristas);
- grafo acíclico, es un grafo que no contiene ciclos (o circuitos), el gráfico presentado como grafo dirigido es acíclico;
- grafo etiquetado (o valorado) es un grafo dirigido con pesos definidos en sus aristas;
- grafo conexo, aquél para el que, tomando cualquier par de vértices que lo forman, existe un camino que los contenga;
- grafo simple, es aquél que entre cada par de vértices existe a lo sumo una arista;
- multigrafo, el caso contrario al grafo simple.
- subgrafo, es el formado por un subconjunto de vértices y aristas contenidos en el grafo del que deriva.
- árbol libre, es un grafo acíclico, conexo y no dirigido. Estos árboles no tienen raíz y los hijos no están ordenados. Para obtener un árbol general hay que seleccionar un nodo como raíz y establecer algún orden entre los hijos de cada nodo.
Subgrafos no dirigidos
Un subgrafo conexo maximal, es un grafo G' que deriva de G, que está contenido, de ninguna forma, en otro subconjunto posible de G. Por ejemplo:
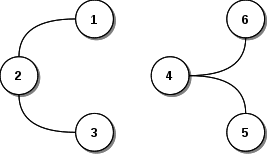
Este subgrafo (G), puede contener a dos subgrafos:
N(G') = { 1, 2, 3 }
A(G') = { <1,2>, <2,3> }
N(G') = { 4, 5, 6 }
A(G') = { <6,4>, <4,5> }Como cada uno de estos subgrafos es máximo, es decir, de forma conexa, no se puede incluir ningún otro nodo del grafo padre que pueda completar más el subgrafo, a cada uno de los subgrafos se les llama conexo maximal.
Se denomina componente conexa de un grafo, a un subgrafo conexo maximal.
En cambio, si el grafo fuese así:
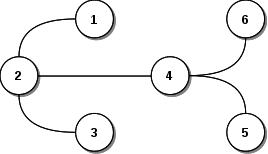
Sería posible, para el primer N(G') agregar el nodo 4, e incluso el 5 o el 6, de modo que, este subgrafo, deja de ser conexo maximal.
El máximo número de aristas en un grafo no dirigido de n vértices es n(n-1)/2. Si tiene ese número de aristas se dice que es completo. No se cuentan los bucles.
Subgrafos dirigidos
El grafo dirigido que no es fuertemente conexo, un subgrafo fuertemente conexo maximal recibe el nombre de componente fuertemente conexa del grafo. El ejemplo tiene dos componentes fuertemente conexas:
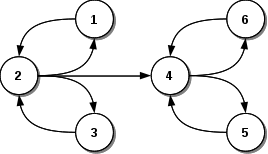
Las dos componentes fuertemente conexas serían:
N(G') = { 1, 2, 3 }
A(G') = { <1,2>, <2,1>, <2,3>, <3,2> }
N(G') = { 4, 5, 6 }
A(G') = { <6,4>, <4,6>, <4,5>, <5,4> }El máximo número de aristas en un grafo dirigido de n vértices es n(n-1). No teniendo en cuenta los bucles.
Representación de los Grafos
Los grafos se pueden representar de varias formas, pero las dos más comunes son: la matriz de adyacencias y la lista de adyacencias.
Matriz de adyacencia
Se crea una matriz (la llamaremos MA por Matriz de Adyacencias) asociada a G, de modo que tenga n x n elementos. Indicaremos sus contenidos con 0 y 1, siendo 1 que en la posición MA[i,j] existe una arista y 0 lo contrario.
Un ejemplo, viendo este grafo dirigido:

Su matriz de adyacencia sería la siguiente (teniendo en cuenta las filas como el origen y las columnas como el destino):
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | 1 | |||||
| 2 | 1 | 1 | ||||
| 3 | 1 | |||||
| 4 | 1 | 1 | ||||
| 5 | ||||||
| 6 | 1 |
En los grafos no dirigidos cada arista es simétrica. En el caso de los grafos valorados, los valores que se representan en la tabla ya no serían 0 y 1, sino el valor del peso de cada arista.
Determinar cuántas aristas hay en un grafo tiene un coste de O(n<sup>2</sup>), y requiere de un espacio de memoria de θ(n<sup>2</sup>). Por lo que no es aconsejado si hay pocas aristas.
Listas de adyacencia
Se representa por un vector de n listas, siendo n el número de nodos, por lo que contiene tantas listas como nodos hay en el grafo. Por lo que el grafo que se muestra a continuación:

Tendrá esta representación en formato de listas de adyacencia:
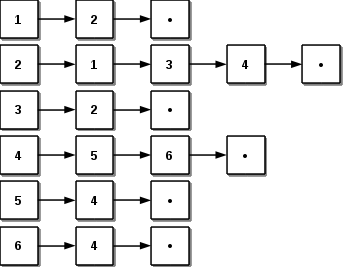
En el caso de los grafos etiquetados, las listas deberían incluir un campo adicional para almacenar la etiqueta asociada a cada arista.
Determinar si existe una arista entre el nodo i y el nodo j puede llevar un tiempo de O(n), ya que puede haber n vértices en la lista asociada de ese vértice en concreto. El coste en espacio de esta representación está en θ(n+a), siendo n el número de nodos y a el número de aristas.
Conclusiones
Hasta aquí he querido llegar de momento en este tema de los grafos. La parte de algoritmia, costes asociados y demás elementos, lo dejo para el siguiente día de estudio.