Pues sí, otra vez de exámenes, otra vez estudiando, y llego a un apartado, en el que lo que decía el libro me sorprende y, al implementarlo, me confirmo. La teoría o lo que viene en los libros no es 100% fiable, en caso de teorías matemáticas, físicas o de computación, hay que comprobar lo que nos indican los libros, porque podemos encontrarnos con una errata.

Actualización: si quieres ver cómo realizar el código del montículo con Elixir, puedes ver esta entrada.

Teniendo en cuenta que lo que indica el libro es un pseudocódigo, es peor aún, puesto que quien lo escribe está seguro de hacerlo bien, y no dudo que incluso lo haya comprobado, pero claro, nos encontramos con que, como no es un lenguaje concreto, pueda ser una interpretación de una implementación, para la cual, se ha podido perder algo de sustancia por el camino, o cometer un error tipográfico.

Pero al grano. Montículos.

¿Qué es un montículo?

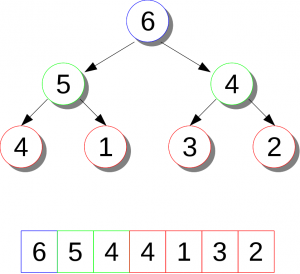
Un montículo es un árbol binario balanceado que cumple con la premisa de que: ningún padre tiene un hijo mayor (montículo de máximos) o menor (montículo de mínimos) a él. Una definición corta y concreta, ¿no?

Esta estructura de datos fue propuesta por Robert W. Floyd (premio Turing en 1978) para resolver el problema de la ordenación de elementos dentro de un vector, el famoso heapsort (u ordenación por montículo).

En la asignatura de Programación y Estructuras de Datos Avanzadas (en la carrera de Grado en Ingenería Informática de la UNED), se propone al inicio de la asignatura, como conocimiento de las estructuras de datos, el montículo.

El montículo, aunque conceptualmente se dibuja en forma de árbol, está implementado sobre un vector. Ya que es balanceado y binario, un nodo solo puede contener dos hijos. La formula para acceder a cada hijo, dado el índice del padre (i), sería:

hijo_izquierdo = 2i
hijo_derecho = 2i + 1

El acceso al padre se realizaría con una división entera: i / 2.

¿Para qué sirve un montículo?

El montículo se emplea en lenguajes de alto y medio nivel, muchas veces sin darnos cuenta. En Java, por ejemplo, se implementa a través de la clase PriorityQueue, la cual permite, a través de un comparador, implementar la ordenación interna del montículo. En otros lenguajes puede aparecer igualmente como cola de prioridad (PriorityQueue) o como montículo (Heap).

El montículo en sí permite:

• Ordenar elementos de un vector de forma fácil y óptima, pudiendo implementar un comparador a medida.
• Búsquedas el máximos, mínimos, o cualquier otro factor a tener en cuenta en la selección de búsqueda de elementos.
• En problemas específicos de grafos como el recubrimiento mínimo de Prim o el camino más corto de Dijkstra.

Implementación del algoritmo

Me ha costado un poco decidir el lenguaje en el que implementarlo, finalmente, he optado por Ruby, ya que su código queda bastante pseudocodificado, pero igualmente habría quedado igual de bien en Python. El código sería:

class MonticuloMaximos
end

Vale, esto es lo básico, la definición de la clase. Ahora vamos a ir creando los métodos:

• inicializador (o constructor): inicializa el vector interno, de modo que en el momento de crear el montículo, este estará vacío:

def initialize()
 @vector = []
end

• vacio?: esta es una de las cosas que más me gusta de Ruby, que puedes poner en un método el símbolo de interrogación, con lo que queda bastante pseudocodificado lo que hace el método en sí. Pregunta si el montículo está vacío, y la respuesta será lógica: sí o no (verdadero o falso):

def vacio?()
  (@vector.length == 0)
end

• flotar: aquí ya comenzamos con las acciones básicas de un montículo. La acción de flotar, se emplea cuando se agrega un elemento nuevo a la estructura. Lo más simple, dado que el montículo se implementa en un vector, es agregar al final del vector el elemento y flotarlo, hasta que su peso nos diga que está en el lugar idóneo, esto hace que el coste del algoritmo sea lineal, y por lo cual, óptimo:

def flotar(i)
  padre = i / 2
  while (i > 1 and @vector[padre - 1] < @vector[i - 1])
    @vector[i - 1], @vector[padre - 1] = @vector[padre - 1], @vector[i - 1]
    i = i / 2
    padre = i / 2
  end
end

• hundir: sería la contrapartida a flotar. En este caso, lo que se hace es que, si eliminamos la cima del montículo, la acción rápida, sería mover el último elemento del vector al principio, cambiar el dimensionamiento del vector y realizar este algoritmo para llevar (o hundir) al elemento a su posición correcta. Igualmente, el algoritmo es lineal:

def hundir(i)
  begin
    hi = 2 * i
    hd = 2 * i + 1
    p = i
    if (hd <= @vector.length and @vector[hd - 1] > @vector[i - 1])
      i = hd
    end
    if (hi <= @vector.length and @vector[hi - 1] > @vector[i - 1])
      i = hi
    end
    if (p != i)
      @vector[p - 1], @vector[i - 1] = @vector[i - 1], @vector[p - 1]
    end
  end until p == i
end

• insertar: en este método, insertamos (como bien dijimos en flotar) un elemento en la estructura, por lo que, hacemos eso mismo, agregamos el elemento y lo flotamos:

def insertar(e)
  @vector.push(e)
  flotar(@vector.length)
end

• primero: nos da el primer elemento del montículo (la cima), pero sin eliminarlo de la estructura. Por lo que el algoritmo es:

def primero()
  @vector[]
end

• cima: igual que el anterior, pero eliminando el elemento de la cima. Para ello, como se comentó en hundir, se toma el último elemento, se inserta en la cima (que queda vacía) y se hunde hacia su posición correcta. El algoritmo sería:

def cima()
  e = @vector[]
  if @vector.length > 1
    @vector[] = @vector.pop
    hundir(1)
  else
    @vector = []
  end
  e
end

• Como ayuda o soporte vamos a crear dos métodos más, uno genérico a Ruby (y presente en otros lenguajes como Java, PHP y Python, pero con distinto nombre) que permite tener una representación en formato texto (o cadena, o string) del montículo: to_s; y otro método que nos dará los elementos del montículo en un vector ordenado (eliminándolos del montículo, claro): ordenado; la implementación de ambos:

def to_s()
  "[ " + @vector.join(", ") + " ]"
end

def ordenado()
  a = []
  a.push cima while not vacio?
  a
end

Una vez visto todo el código, podemos hacer una prueba como la siguiente, en la que insertaremos unos datos aleatorios y obtendremos el resultado de su almacenamiento en forma de montículo, y el resultado en un vector ordenado:

a = [ 6, 4, 3, 1, 5, 2, 4 ]

m = MonticuloMaximos.new
a.each do |e|
  m.insertar(e)
end

puts m

puts "[ " + m.ordenado.join(", ") + " ]"

El resultado es el siguiente:

[ 6, 5, 4, 1, 4, 2, 3 ]
[ 6, 5, 4, 4, 3, 2, 1 ]

NOTA: Como se podrá ver en la implementación, este código estaba preparado para vectores que enumerasen sus elementos en base a 1..N, y sin embargo, todos los lenguajes (a excepción de Pascal, Modula-2, y otros similares) numeran los vectores de 0..N-1, por lo que en cada acceso al atributo @vector se ha tenido que decrementar en 1 el número, para pasar de la notación 1..N a 0..N-1.

Conclusiones

El montículo es un gran elemento que se sigue empleando por su simpleza y óptima respuesta, ya que en lugar de emplear estructura de árbol, grafos o listas, emplea un simple vector, por lo que cada acción a realizar sobre él resulta con un coste bastante reducido. Así mismo, como había dicho al principio, esté presente en todos los lenguajes, ya sea con el nombre de heap, o PriorityQueue, con la capacidad de poder implementar su comparador (para máximos, mínimos o a medida), por lo que no hay excusa para no emplearlo cuando la situación lo requiera.