Montículos con Elixir

Hace 7 años escribí una entrada mientras estudiaba los montículos para la asignatura de Programación y Estructuras de Datos Avanzadas de la UNED. Al revisar la entrada y ver que aún hay mucha gente consultando he decidido retomarla y actualizarla pero además he creado esta entrada para ver cómo se haría en Elixir, ¿te animas a ver los montículos en Elixir?

Prefiero que leáis la otra entrada para todo el tema teórico sobre los montículos y centrar esta entrada solo en la parte que concierne a Elixir. Solo comentaré de los montículos la definición.

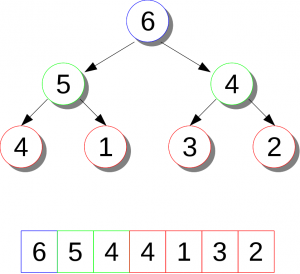
Un montículo es un árbol binario balanceado que cumple con la premisa de que: ningún padre tiene un hijo mayor (montículo de máximos) o menor (montículo de mínimos) a él. Una definición corta y concreta, ¿no?

El montículo, aunque conceptualmente se dibuja en forma de árbol, está implementado sobre un vector. Ya que es balanceado y binario, un nodo solo puede contener dos hijos. La formula para acceder a cada hijo, dado el índice del padre (i), sería:

hijo_izquierdo = 2i
hijo_derecho = 2i + 1

El acceso al padre se realizaría con una división entera: i / 2.

Implementación del algoritmo

El código base para el módulo empleando Elixir sería:

defmodule MonticuloMaximos do
end

Ahora vamos a ir creando las funciones para agregarlas dentro de esa especificación:

nuevo: crea un montículo. La idea es que retorne la estructura para el montículo vacío. Como empleamos una lista para implementar el montículo, retornaremos una lista vacía:

def nuevo, do: []

vacio?: pregunta si el montículo está vacío y la respuesta será lógica: sí o no (veradero o falso):

def vacio?(monticulo) do
  monticulo == []
end

flotar: aunque los libros de texto nos digan que la opción óptima es realizar una inserción en la lista en el último elemento y después flotar esto no es correcto para Elixir ni otros lenguajes funcionales. Lo ideal en este caso es agregar el elemento a la cabeza y hundirlo. Lo veremos en la inserción.
hundir: igualmente hundir no tiene sentido cuando eliminamos la cima porque la lista se ajusta dinámicamente cuando eliminamos la cabeza en Elixir. Lo veremos en la implementación de cima.
insertar: en esta función insertamos un elemento en la estructura buscando el lugar óptimo para él. La implementación simplemente es creando una lista vacía como nuevo parámetro e iterar el montículo insertando los elementos menores en él hasta encontrar un elemento igual o mayor, entonces se agrega el elemento y el resto.

def insertar(monticulo, elemento) do
  insertar(monticulo, [], elemento)
end

def insertar([], elementos, elemento), do: elementos ++ [elemento]
def insertar([a1|a], elementos, elemento) when a1 > elemento do
  insertar(a, elementos ++ [a1], elemento)
end
def insertar(a, elementos, elemento) do
  elementos ++ [elemento|a]
end

primero: nos da el primer elemento del montículo (la cima) sin eliminarlo:

def primero([elemento|_]), do: elemento

cima: igual que el anterior pero elimina el elemento de la cima. Debemos retornar una tupla con el primer elemento siendo la cima y el resto con el contenido restante:

def cima([elemento|monticulo]), do: {elemento, monticulo}

Una vez visto todo el código, podemos hacer una prueba como la siguiente, en la que insertaremos unos datos aleatorios y obtendremos el resultado de su almacenamiento en forma de montículo, y el resultado en un vector ordenado:

iex> a = [ 6, 4, 3, 1, 5, 2, 4 ]
[ 6, 4, 3, 1, 5, 2, 4 ]

iex> m = MonticuloMaximos.nuevo
[]

iex> f = fn(e, m) ->
...>   MonticuloMaximos.insertar(m, e)
...> end
#Function<12.99386804/2 in :erl_eval.expr/5>

iex> List.foldl(a, m, f)
[6, 5, 4, 4, 3, 2, 1]

En esta versión no necesitamos de extraer o presentar la información. Está implementada usando una lista y eso nos da la ventaja de poder imprimirla por pantalla en la consola simplemente poniendo el valor o dentro de un texto con el uso de inspect.

Conclusiones

Realmente si queremos seguir las indicaciones del libro de texto que enseña a programar en lenguajes imperativos nos encontraremos ciertas contradicciones o puntos de inflexión donde los algoritmos no funcionan tal y como vienen expuestos. Comentaré algo en un futuro cercano. Por el momento me quedo con la simplicidad de ver cómo el código escrito en Elixir es igual de funcional que el escrito en Ruby y mucho más corto y manejable.

¿Y tú? ¿Has jugado con algoritmos básicos o de estructuras de datos entendidas para lenguajes imperativos en lenguajes funcionales? ¿Has tenido alguna experiencia buena o mala con el cambio? ¡Déjanos tu comentario!